Hangkártyák programozása retro 22.

8.3. A Fourier térben végezhető konvolúció C függvénye

A következő struktúra definiálása szükséges:

typedef struct { int n;         // A függvény elemek száma

int n0;        // Az első elem valódi indexe

double *fv;    // Mutató a függvény elemek tömbjére

int ndft;      // A dft alappontok száma, vagy 0

complex *dft;  // Mutató a dft értékekre, vagy NULL

} fvtype;

A függvény az fvtype struktúrákban a Fourier transzformáltat is tárolja, azt csak akkor számolja újból, ha szükség van rá.

extern “C” __declspec(dllexport)

int WINAPI convol_by_fft(fvtype *fvta,fvtype *fvtb,fvtype *fvtres)

// A bemenő függvényeket és az eredmény függvényt kapja paraméternek

{ long int i,na,nb,nres,ndft,logndft;

double s,*dbuff,*dp1,*dp2;

complex *cp1,*cp2,*cp3;

//Előkészítések

na=fvta->n;

nb=fvtb->n;

nres=na+nb-1; //Az eredmény vektor hossza

ndft=1; //A DFT hossza

logndft=0;

while(ndft<nres) { ndft<<=1; logndft+=1; }

refft_prepare(logndft); //Az FFT előkészítése

//Operandusok transzformálása

if(dft_fvtype(fvta,ndft)) goto alloc_err;

if(dft_fvtype(fvtb,ndft)) goto alloc_err;

//Konvolúció

free_fvtype(fvtres);

fvtres->dft=(complex*)farcalloc(ndft,sizeof(double));

if(fvtres->dft==NULL) goto alloc_err;

cp1=fvta->dft;

cp2=fvtb->dft;

cp3=fvtres->dft;

cp3->re=cp1->re*cp2->re;

cp3->im=cp1->im*cp2->im;

cp1++; cp2++; cp3++;

for(i=1;i<ndft/2;i++) cx_mul(cp1++,cp2++,cp3++);

fvtres->ndft=ndft;

//Visszatranszformálás

dbuff=(double*)farcalloc(ndft,sizeof(double));

if(dbuff==NULL) goto alloc_err;

dp1=(double *)fvtres->dft;

dp2=dbuff;

s=(double)ndft;

for(i=0;i<ndft;i++) *(dp2++)=*(dp1++)*s;

reifft(dbuff);

//Az eredmény elhelyezése az eredményvektorban

fvtres->fv=(double*)farcalloc(nres,sizeof(double));

if(fvtres->fv==NULL) goto alloc_err2;

dp1=dbuff;

dp2=fvtres->fv;

for(i=0;i<nres;i++) *(dp2++)=*(dp1++);

fvtres->n=nres;

fvtres->n0=fvta->n0+fvtb->n0; //Kezdőpont offset

//Kilépések, hibajelzések

farfree(dbuff);

refft_close();

return(0);

alloc_err2:

farfree(dbuff);

alloc_err:

refft_close();

return(1);

}

A fenti függvény szintén megtalálható a F.27-ben.

A Delphi-ben közvetlenül alkalmazott C függvények deklarálása, illetve rövid leírása:

function ReFftPrepare(log_n:longint):integer;

stdcall; external ‘prjconvoldll.dll’ name ‘refft_prepare’;

A fenti függvény feladata, hogy előkészítse a bemenő valós vektor transzformációjához szükséges munkaterületeket és az exponenciális függvény táblázatos kezelését. A transzformáció elvégzése előtt mindig ezt a függvényt kell meghívni, s itt kell megadni, hogy hány alappontú transzformációt szeretnénk végezni.

procedure ReFftClose;

stdcall; external ‘prjconvoldll.dll’ name ‘refft_close’;

A ReFfftClose függvény, illetve eljárás a ReFftPrepare által lefoglalt munkaterületek felszabadítását végzi, ha már nem kívánunk további transzformációkat végezni.

procedure ReFft(poi:pdouble);

stdcall; external ‘prjconvoldll.dll’ name ‘refft’;

Ez az eljárás végzi a valós bemenő vektor gyors Fourier transzformációt, miután megtörtént a munkaterületek előkészítése és az exponenciális függvény táblázatos megadása. Algoritmusát és az azt megvalósító program kódját részletesen tárgyaltuk az előző fejezetekben.

procedure ReiFft(poi:pdouble);

stdcall; external ‘prjconvoldll.dll’ name ‘reifft’;

A ReiFft eljárás végzi az inverz gyors Fourier transzformációt, amely szintén a szükség előkészítések után végezhető el eredményesen. Paraméterként a transzformálandó vektor kezdetére mutató pointert vár.

procedure InitFvtype(fvt:pfvtype);

stdcall; external ‘prjconvoldll.dll’ name ‘init_fvtype’;

A fenti eljárás a kezdeti, üres állapotnak megfelelően kitölti az fvt struktúrát, illetve rekordot. Deklarációt követően használata kötelező, de a tapasztalat azt mutatja, hogy a Delphi eleve az üres állapotnak megfelelően tölti ki a struktúrát, vagyis elvégzi helyettünk az inicializálást. Delphi-ben használata inkább ajánlatos, mint kötelező érvényű.

function FillFvtype(n:longint;n0:longint;data:pdouble;fvt:pfvtype):integer;stdcal;external ‘prjconvoldll.dll’ name ‘fill_fvtype’;

A megfelelő adatsor alapján a FillFvtype függvény kitölti az adott struktúrát, illetve rekordot.

function Convolution(fvta:pfvtype;fvtb:pfvtype;fvtres:pfvtype):integer;

stdcall; external ‘prjconvoldll.dll’ name ‘convol_by_fft’;

A tulajdonképpeni konvolúciót végző függvény, amelynek mindhárom paramétere egy fvtype típusú rekord. A rutin meghatározza a konvolúció eredményének hosszát és az FFT alappontjainak minimálisan szükséges hosszúságát, majd előállítja a két operandus transzformáltját. Kiszámítja az operandusok DFT-inek szorzatát, és ezt az eredmény DFT mezőjére helyezi. Végül elvégzi az eredmény visszatranszformálását.

A következő metódus magának, a konvolúciónak a teljes menetét mutatja be:

procedure TForm1.Convolution1Click(Sender: TObject);

var i:longint;

begin

//A kurzorunk jelzi, hogy dolgozunk

screen.cursor:=crHourglass;

try

//Függvények inicializálása

InitFvtype(@fv1);

InitFvtype(@fv2);

InitFvtype(@fv3);

//Az operandus függvények előkészítése, hiba esetén jelzés, majd kilépés

if(FillFvtype(high(p1^)+1,0,@p1^,@fv1))<>0 then

begin

ShowMessage(‘Allocation error while FillFvtype!’);

exit;

end;

if (FillFvtype(high(p2^)+1,0,@p2^,@fv2))<>0 then

begin

ShowMessage(‘Allocation error while FillFvtype!’);

exit;

end;

//Konvolúció elvégzése, hiba esetén jelzés, majd kilépés

if (Convolution(@fv1,@fv2,@fv3))<>0 then

begin

ShowMessage(‘Allocation error while Convolution!’);

exit;

end;

//A konvolúció eredményének kiolvasása

for i:=low(pres^) to high(pres^)-1 do

begin

pres^[i]:=fv3.fv^;

inc(fv3.fv);

end;

//Ha végeztünk üzenet, illetve a kurzor visszaállítása

ShowMessage(‘Convolution ready!’);

finally

screen.cursor:=crDefault;

end;

button:=3;

//Az eredmény függvény grafikus megjelenítése

DrawWaveRes(pres^);

end;

Egy, az FFT elvégzésére alkalmas metódust is bemutatok:

procedure TForm1.normal1Click(Sender: TObject);

begin

//Jelölések tájékoztatásul: most normal FFT-t végzünk

normal1.checked:=true;

inverse1.checked:=false;

screen.cursor:=crHourGlass;

try

//A transzformálandó függvény kiválasztása

case button of

1:

begin

// Munkaterület, exp.tábla előkészítése,

// transzformáció alappontjainak száma

if ReFftPrepare(lognfft)<> 0 then

begin

ShowMessage(‘Allocation error while FFT!’);

exit;

end;//if

//Gyors Fourier transzformáció elvégzése

Refft(@p1^);

//Lefoglalt munkaterületek felszabadítása

ReFftClose;

//A transzformált grafikus megjelenítése

DrawWaveSam(p1^);

end;//1

2:

begin

if ReFftPrepare(lognfft)<> 0 then

begin

ShowMessage(‘Allocation error while FFT!’);

exit;

end;//if

Refft(@p2^);

ReFftClose;

DrawWaveSam(p2^);

end;//2

3:

begin

if ReFftPrepare(lognfft+1)<> 0 then

begin

ShowMessage(‘Allocation error while FFT!’);

exit;

end;//if

Refft(@pres^);

ReFftClose;

DrawWaveRes(pres^);

end;//3

end;//case

finally

screen.cursor:=crDefault;

end;

end;

Lejjebb, F.24-ben példát láthatunk a konvolúció eredményére.

A konvolúciót, illetve az FFT-t végző teljes Delphi forrás pedig a F.28-ban tanulmányozható.

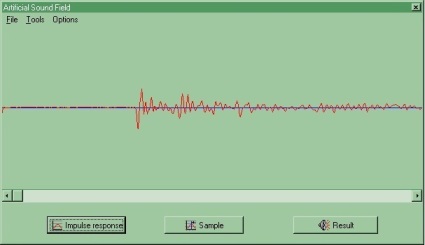
Impulzusválasz függvénye

Tetszőleges gerjesztés függvénye

Konvolúció eredménye

F.24. Mesterséges hangzás megvalósítása konvolúcióval

Hírdetés